To Invest or Pay Down Debt, That is the Question
 One of my favorite Will Rogers quotes is: “Don’t gamble; take all your savings and buy some good stock and hold it till it goes up, then sell it. If it don’t go up, don’t buy it.” Seems like sage advice to me, and it’s about as helpful as the canned response I give when I’m asked the following:
One of my favorite Will Rogers quotes is: “Don’t gamble; take all your savings and buy some good stock and hold it till it goes up, then sell it. If it don’t go up, don’t buy it.” Seems like sage advice to me, and it’s about as helpful as the canned response I give when I’m asked the following:
“I’ve got some money/income – should I use that to pay down my mortgage or should I put it to work in the market?”
My response of “It depends on whether the market is going to go up or down” is likely not very helpful, but it does elicit some entertaining brow-furrowing.
From a purely mathematical standpoint, paying off a debt that is compounding at one rate (after tax) is exactly the same as investing money at the same rate (after tax). Paying off a higher interest debt is, other things equal, better than investing money at a lower rate of return. And, investing money at a higher rate is better than paying off lower-interest debt. Most of the time, though, simple fact is that we just don’t know the rate of return on an investment (or a portfolio of investments) ahead of time.
From a planning standpoint, advisors will often use an “expected rate of return” to compare with the cost of debt in order to make a recommendation. Often this return expectation comes from past performance of similar investments. Example: Jane has a mortgage at a 3.75% rate, and has enough to pay it down. John, her advisor assumes a 5% annual rate of return on her investment portfolio. Given this assumption he recommends that she not pay her mortgage off, but rather invest the money.
The problem with this approach is that there could very well be a situation where Jane is disappointed at the end, because the investment doesn’t perform along the lines of the expectation laid out by the advisor, and she looks back and realizes she would have been better off paying off the mortgage. While Joe probably had a good basis in assuming an “expected” rate of return on the investment, the reality is that there is a near-certainty that the ACTUAL rate of return will NOT equal the expected rate. It will almost certainly be higher or lower.
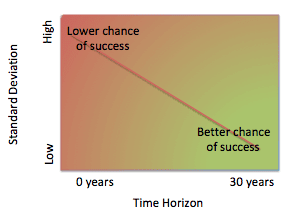
A better approach, and one which we espouse, is to consider both the expected rate of return and the variability of returns. Statistics geeks refer to this variability as ‘standard deviation’, and this number can be measured with the help of software. Once an advisor has determined the standard deviation of an investment and the number of years to run the equation, the probability of investing beating debt pay-down can be calculated. With that number in mind, the investor can make a subjective decision on whether the probability of success is high enough to risk the money in an investment portfolio.
If the investment is expected to return a higher amount than debt cost, both the amount of difference between the two AND the standard deviation are going to have an impact on the likelihood of success in an investment scenario. Standard deviation increases as the level of market risk increases in a portfolio. So, a portfolio with more stocks is going to have higher standard deviation than a portfolio with more bonds or cash. Interestingly, the higher the time horizon, the lower the variability of returns in a portfolio (take into account that the market has experienced a lot of one year declines, but not many 30 year declines!). So a combination of lower portfolio volatility and longer time horizon weigh positively on the decision to invest rather than to pay off debt. Unless there is a significant difference between the expected rate of return and the debt rate, a more variable investment with a shorter time horizon might not be worth the risk to most investors, relative to paying down the debt.
 Taxes are another consideration, since both the cost of debt and potential investment return should be considered in after-tax numbers. Interestingly, with the Tax Cuts and Jobs Act of 2017 creating a universe where far fewer people will be itemizing, the after-tax impact of mortgage interest is likely to be higher for many people. That and markets with overall lower expected nominal rates of return and higher volatility may tilt the scale more toward debt pay-down and away from investing for some potential investors facing the choice.
Taxes are another consideration, since both the cost of debt and potential investment return should be considered in after-tax numbers. Interestingly, with the Tax Cuts and Jobs Act of 2017 creating a universe where far fewer people will be itemizing, the after-tax impact of mortgage interest is likely to be higher for many people. That and markets with overall lower expected nominal rates of return and higher volatility may tilt the scale more toward debt pay-down and away from investing for some potential investors facing the choice.
All things considered, this would be a much easier decision to make if we simply knew exactly what the markets would do… But since that’s never going to be the case, looking at this as an exercise in probability (and, after all isn’t EVERYTHING an exercise in probability?) is the healthiest way of coming to a comfortable decision when facing the challenge of how to deploy that extra income or asset.



